This is the teacher guide for this lesson. A student-focused guide to assist learners as they perform the activity is available.

Entangled and shuffled
Exploring quantum correlations and entanglement through tabletop games
What makes quantum particles and systems different from normal objects?
- Provided in kit:
- Deck of playing cards
- Pen/pencil and paper
- S index calculating boards (one per student pair - laminated or in sheet protectors)
- Teacher provided:
- Dry erase markers
- Dry erase board cleaner
Objectives:
Students will be able to:
- Model connections between regular items like playing cards and the behavior of quantum particles
- Calculate correlations for non-entangled and entangled scenarios using playing cards
- Total time30 - 45 min for activity. More time needed for mini-lesson and interpretation.
- Education levelGrades 6 - 10
- Content AreaComputer science, quantum information science
- Educational topicQuantum correlations, superposition, entanglement
What is Quantum Information Science (QIS)?
The field of Quantum Information Science (QIS) is a multidisciplinary area of research that is positioned right in between science, engineering and technology. It studies how we can take advantage of the unique properties of quantum systems for technological and informational applications such as creating new and better computers, developing digital networks with better encryption protocols, and creating sensors and measuring devices with enhanced precision.
Why is QIS important?
During the last century, the development of lasers and transistors led to an explosion in the availability of technology and information circulating around the world. This has strongly reshaped our societies, defining a new “information age.” Effectively, all the information and data that we use is currently stored, transmitted and processed through standard ("classical") methods that involve the manipulation of electronic states that are interpreted as “ON” or “OFF,” "0" or "1" – states of information known as bits.
The complexity of these information systems is not a feature of the fundamental parts of our computers, but rather only a result of the enormous scale of both the number and speed at which bits are processed in our devices. A significant challenge, however, relies on the fact that the amount of memory and processing power required to handle and analyze large systems scales exponentially. This means that as our information systems keep expanding, the amount of resources required to run these systems will become unsustainable in the long term. The hope is that QIS can provide a solution to this problem.
What distinguishes quantum technologies from regular devices?
We can identify three “ingredients” that distinguish quantum technologies from regular devices:
1) Superposition: While a bit can have a value of either zero or one, a quantum bit (qubit) can have a value that is either zero, one or a quantum superposition of these values. In a state of superposition, the value of the qubit cannot be described as either zero or one in a definite way. Given two bits, a regular computer can store four possible different values (zero zero, zero one, one zero, or one one), although only one of those at a time. Given two qubits, in principle all four values can be represented simultaneously. Mathematically, we represent this as:
|⟩=a|00⟩+ b|01⟩+c|10⟩+d|11⟩
Each bracket |⟩ (“ket” for short) represents a state on which the system can be, and the fact that they are added together indicates the superposition.
2) Correlations: the state of a qubit can be readily affected by its interaction with other elements in the system, influencing the probability of a certain outcome during experiments. Given the right circumstances, a particular combination of states might prevent certain outcomes through destructive quantum interference.
3) Entanglement: Entanglement is a stronger, more specific form of correlation where particles are linked in a way that their fates are intertwined, even when separated by large distances. When qubits become entangled, they form a “global” system such that the quantum state of different parts of the system cannot be described independently. We therefore say that there exist specific correlations between each of the components.
A key insight to understand the advantages of quantum systems consists in realizing the similarity between the superposition of quantum states (|00⟩+ |01⟩+ |10⟩+… ) and the way a classical parallel computer runs, where many different inputs are processed within the time of a single calculating cycle. However, unlike the stack of Central Processing Units that is necessary to run a classical parallel computation, a single quantum system has the potential to provide parallel processing as a “built-in” feature. Initially, this suggests the possibility of carrying out these calculations with a much smaller number of resources and a method to bypass the exponential explosion problem.
How can we use tabletop games to explain QIS?
Given that studying quantum systems is both technically and conceptually challenging, QIS topics and concepts are not usually discussed until students take advanced undergraduate and graduate level classes. However, it is possible to highlight the key differences between classical and quantum systems by using items commonly found in tabletop games such as cards. We think the fact that these items are easily accessible should help to make the quantum concepts more relatable to young students and a general audience.
- If two particles that have a spin sum of zero have “hidden variables” that can describe their spin before the measurement, then there’s a known limit to how often we can measure both of the particles as having a positive spin (on any axis… any axis??)
Teacher tips:
- Suggested STEP UP Everyday Actions to incorporate into the activity.
- Consider using whiteboards during discussions, so students have time to brainstorm and work through their ideas before saying them out loud.
- As students experiment, roam around the room to listen in on discussion and notice experiment techniques. If needed, stop the class and call over to a certain group that has hit on an important concept.
- Consider these responsive tools and strategies and/or open ended reflection questions to help push student thinking, and to help students track their thinking during the activity.
- Connect to students’ lives and create opportunities to develop STEM identity using these suggested extensions.
- Allow the work of physicists to come alive by signing up for a virtual visit from a working physicist using APS’ Physicist To-Go program. You can request a quantum physicist to talk about the concepts students learned in this activity!
Students will model superposition, correlations, and entanglement of particles using playing cards. This will help students visualize and understand basic properties of quantum information science.
We invite you to watch a brief video demonstration of the developer conducting the experiment you’ll be facilitating with your students.
For teachers who are less familiar with quantum superposition and Bell’s inequality, watching this video may provide helpful background information.
Consider exploring Elisa Torres Durney’s scientific profile using the lesson’s ideas detailed on the Introduction found in your materials kits.
Prepare a few decks of cards that are randomly shuffled.
Prepare a few decks of cards that are arranged in a specific color pattern (ex. all red, all black, alternating colors, two blacks then two reds, etc.)
Ask students what they think it means for particles to be “entangled.” Let them know this is a new concept they probably haven’t learned about so their ideas are all just brainstorms.
Pass out part of a normal, randomly shuffled deck (labeled deck one) of cards to each student group.
Pass out part of a deck arranged in a specific pattern (labeled deck two) to each student group.
Give each student group a copy of the S index worksheet (for part two).
Introduce the mathematical idea of a correlation index, that is a number that has a meaning depending on the outcomes of the events:
- +1 if the colors of the cards match (ex. red-red or black-black)
- -1 if the colors of the cards don’t match (red-black)
Hand out shuffled, randomized decks to each group. Ask students to divide the cards into two parts
The students will now start drawing pairs of cards, one from each of the decks. Ask them to compare their colors and to evaluate and write down the correlation index for each case.
Have them record their observations for deck one and deck two in their notebooks.
Discuss with the students what kind of pattern they observed.
There should be no pattern to the correlations between them, and no way to predict what the outcome will be. This is an uncorrelated system.
Now repeat the exercise, but instead hand out the decks that you pre-arranged in some specific color pattern. Once the students have made several pairs, the outcomes become predictable. This is a correlated system.
Online version
There is an online version of this section of the activity that can be found here.
Hand each team part of a shuffled deck of cards.
Each group draws four cards from the shuffled deck and lays them on the board.
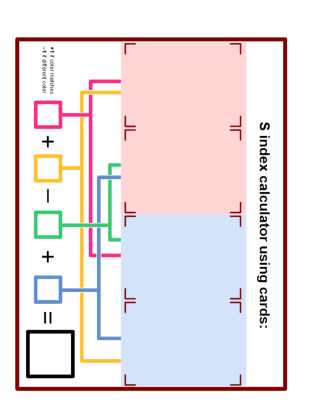
Ask them to start flipping the cards in pairs and calculating the correlation indices according to the rule:
- Same color = +1
- Different color = -1
Add the four different correlation indices using the pattern C1 + C2 – C3 + C4 as indicated on the board.
Take the absolute value of the outcome. We will refer to the result as the “S index.”
Example
 Initial draw
Initial draw First pair: red and black, so C1 = -1
First pair: red and black, so C1 = -1 Second pair: red and red, so C2 = +1
Second pair: red and red, so C2 = +1Third pair: red and black, so C3 = -1
Fourth pair: red and red, so C4 = +1
 Final evaluation: S = |C1 + C2 – C3+C4| = 2
Final evaluation: S = |C1 + C2 – C3+C4| = 2Ask each group to share their results. They should all get the result S is equal to two.
Note: sometimes students get a different value than two, but that is due to a calculation error. If that happens, check each of the correlation values. The most common mistake is not to add the four correlation values appropriately (C3 should be subtracted).
Play a few different rounds to motivate the idea that the result is always two.
Present challenge to the students: if you hand-pick cards instead of choosing them randomly, is it possible to get an outcome value larger than two?
Ask the students to argue whether they think that it is possible/not possible to get an S value larger than two. After some discussion, it should become clear that even when hand-picking, it is NOT possible to get a value larger than two. This exemplifies the concept of Bell’s inequality.
For everyday systems, there is a limit that sets a maximum value for correlation indices. In our case the inequality is S is less than or equal to two.
Discuss with the students that the reason for this is that the outcome depends on the colors of the four cards, and their different correlations. Even when the cards are facing down, it is either black or red (similar to a regular computer bit), so once three out of the four cards have been drawn, you immediately know the outcome of the fourth correlation.
This is related to the concept of “reality” in quantum mechanics. In classical systems the bits really are in only one state or another. That is not the case for quantum systems. They are in superposition of states (activities 7 and 8 allow students to visualize this concept). You may want to try those next!
The fact that the situation is presented as a challenge is very engaging for students, and it also shows that there seems to be a “limit” in the maximum correlations that we can get, even after hand-picking the cards. In other words, it is impossible to get a value larger than two.
When the same exercise is carried out using entangled quantum particles such as photons (particles of light) or single atoms at very low temperatures, it is possible to get values of S greater than two, and thus surpass Bell’s inequality. This means that entangled particles are more correlated with each other than they ought to be. In a way, this kind of test can be used to verify if a system is having quantum effects or not. Ask the students to imagine ways in which this could be possible.
Relate this to the idea that if we had “quantum cards,” then we couldn’t properly describe them as being either black or red before looking at them. Pictorially, we can imagine them as constantly fluctuating between being red or black, and we would have to represent them with a video or an animation instead of a picture. In this case, the value will not necessarily add up to two. Or, in other words, because the cards can be in a combination of states, it is possible to get a correlation value (S value) greater than 2, surpassing the classical limit.
Finally, put all the ideas together to relate this example to how quantum technologies work. In the card game, we saw that when playing under the regular rules, there is no way to obtain a value of S greater than two. This is due to the cards being definitely either black or red. Similarly, regular computers work with classical bits, which are also definitely either zero or one. This imposes limits on the capabilities of the computers.
One way in which we can imagine surpassing that limit in the card game is having cards that are not either black or red in a definite way. Similarly, quantum computers work using qubits, and because they can be in a superposition state, they don’t necessarily have a definite state. These additional possibilities allow them to surpass some of the limitations of regular computers.
- There are also many STEM YouTube channels that are great for learning about QIS such as Looking Glass Universe, Qiskit. and AM.
- Sign up for Physicists To-Go to have a scientist talk to your students.
- Use Elisa Torres Durney’s scientist profile to spark conversations about who does quantum physics.
Real world situations/connections can be used as is, or changed to better fit a student’s own community and cultural context.

Quantum Atlas
The Quantum Atlas project is a great starting point for learning more about QIS.

3Blue1Brown
For learning more about math, 3Blue1Brown is one of our favorites.

Career and Workforce Connections: Quantum Careers lesson
Career and Workforce Connections: Quantum Careers lesson (1 - 2 class periods)
Credits
Developed by: Danyel Cavazos - University of Chicago
Piloted by: Kimberly Becker, Ann Marie Dubick, Nataliya Fletcher, Cindy King, Nicholas Sordillo